Interlocking Quoits
 Figure 1 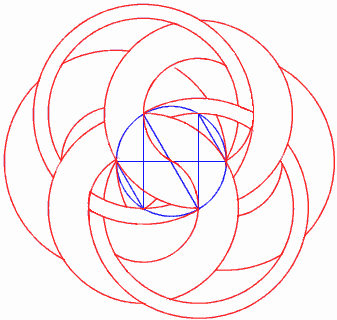 Figure 2 |
I make no claim to have originated this type of pattern. It was derived from the principles laid down in the book The Language of Pattern by Keith Albarn, Jenny Miall Smith, Stanford Steele and Dinah Walker (Page 75).
I have however added the colour and 3-dimensionality that the authors omitted in the book. To create the image you see at Figure 1 I used that wonderful bit of software, Bryce 4. The method of generating these patterns is not at all obvious from the finished products - indeed at first glance they do not look as though they have been created according to a logical scheme at all, but they have. Start with the circumference of a circle (in blue - Figure 2). Divide this into any number of equally sized segments. Connect the vertices with straight lines in a random, continuous loop (trying to ensure that the two chords from each vertice are of different lengths) then draw circles with origins at each vertice and radii equal to the length of the two chords from that point formed by the continuous loop. Then, by the judicious removal of parts of the generated curves a woven series of toruses (quoit shapes) can be seen. The rest is a matter of colour. |